cuSpatial Python User’s Guide#
Contents#
Installing cuSpatial#
Read the RAPIDS Quickstart Guide to learn more about installing all RAPIDS libraries, including cuSpatial.
[1]:
# !conda create -n rapids-24.06 -c rapidsai -c conda-forge -c nvidia \
# cuspatial=24.06 python=3.9 cudatoolkit=11.5
If you wish to contribute to cuSpatial, you should create a source build using the excellent rapids-compose
GPU accelerated memory layout#
GeoArrow buffers, a GPU-friendly data format for geometric data that is well[2]:
# Imports used throughout this notebook.
import cuspatial
import cudf
import cupy
import geopandas
import pandas as pd
import numpy as np
from shapely.geometry import *
from shapely import wkt
[3]:
# For deterministic result
np.random.seed(0)
cupy.random.seed(0)
Input / Output#
The primary method of loading features into cuSpatial is using cuspatial.from_geopandas.
__array_interface__ for coordinates and their feature offsets.cuspatial.from_geopandas#
The easiest way to get data into cuSpatial is via cuspatial.from_geopandas.
[4]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path(
"naturalearth_lowres"
))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
print(gpu_dataframe.head())
/tmp/ipykernel_5364/3038749724.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
pop_est continent name iso_a3 gdp_md_est \
0 889953.0 Oceania Fiji FJI 5496
1 58005463.0 Africa Tanzania TZA 63177
2 603253.0 Africa W. Sahara ESH 907
3 37589262.0 North America Canada CAN 1736425
4 328239523.0 North America United States of America USA 21433226
geometry
0 MULTIPOLYGON (((180.00000 -16.06713, 180.00000...
1 POLYGON ((33.90371 -0.95000, 34.07262 -1.05982...
2 POLYGON ((-8.66559 27.65643, -8.66512 27.58948...
3 MULTIPOLYGON (((-122.84000 49.00000, -122.9742...
4 MULTIPOLYGON (((-122.84000 49.00000, -120.0000...
(GPU)
Geopandas and cuDF integration#
GeoSeries is represented internally using GeoArrow data layout.cuDF.cuDF operation on cuSpatial non-feature columns, and most operations will workgeometry column. Operations that reduce or collate the number of rows in your DataFrame,groupby, are not supported at this time.[5]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
continents_dataframe = gpu_dataframe.sort_values("name")
print(continents_dataframe)
pop_est continent name iso_a3 gdp_md_est \
103 38041754.0 Asia Afghanistan AFG 19291
125 2854191.0 Europe Albania ALB 15279
82 43053054.0 Africa Algeria DZA 171091
74 31825295.0 Africa Angola AGO 88815
159 4490.0 Antarctica Antarctica ATA 898
.. ... ... ... ... ...
2 603253.0 Africa W. Sahara ESH 907
157 29161922.0 Asia Yemen YEM 22581
70 17861030.0 Africa Zambia ZMB 23309
48 14645468.0 Africa Zimbabwe ZWE 21440
73 1148130.0 Africa eSwatini SWZ 4471
geometry
103 POLYGON ((66.51861 37.36278, 67.07578 37.35614...
125 POLYGON ((21.02004 40.84273, 20.99999 40.58000...
82 POLYGON ((-8.68440 27.39574, -8.66512 27.58948...
74 MULTIPOLYGON (((12.99552 -4.78110, 12.63161 -4...
159 MULTIPOLYGON (((-48.66062 -78.04702, -48.15140...
.. ...
2 POLYGON ((-8.66559 27.65643, -8.66512 27.58948...
157 POLYGON ((52.00001 19.00000, 52.78218 17.34974...
70 POLYGON ((30.74001 -8.34001, 31.15775 -8.59458...
48 POLYGON ((31.19141 -22.25151, 30.65987 -22.151...
73 POLYGON ((32.07167 -26.73382, 31.86806 -27.177...
[177 rows x 6 columns]
(GPU)
/tmp/ipykernel_5364/567044009.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
cuspatial.GeoDataFrame and CPU-backedgeopandas.GeoDataFrame with from_geopandas and to_geopandas, enabling you toPolygon associated with the first item in the dataframe sorted[6]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
sorted_dataframe = gpu_dataframe.sort_values("name")
host_dataframe = sorted_dataframe.to_geopandas()
host_dataframe['geometry'].iloc[0]
/tmp/ipykernel_5364/1940355512.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
[6]:
Trajectories#
LineString coupled with a time sample for each point in the LineString.cuspatial.trajectory.derive_trajectories to group trajectory datasets and sort by time.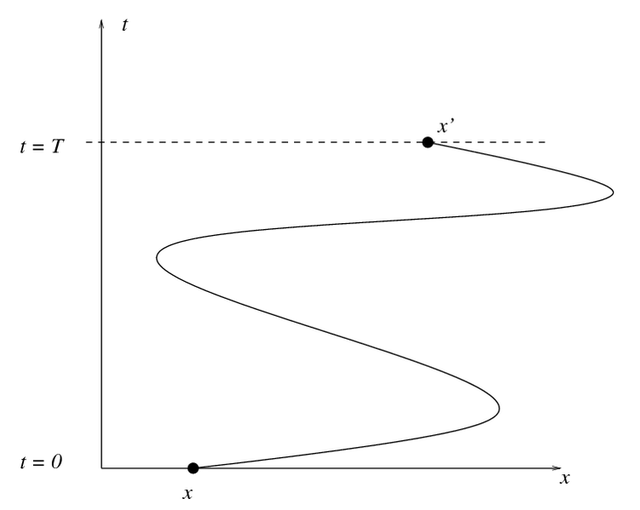
cuspatial.derive_trajectories#
[7]:
# 1m random trajectory samples
ids = cupy.random.randint(1, 400, 1000000)
timestamps = cupy.random.random(1000000)*1000000
xy= cupy.random.random(2000000)
trajs = cuspatial.GeoSeries.from_points_xy(xy)
sorted_trajectories, trajectory_offsets = \
cuspatial.core.trajectory.derive_trajectories(ids, trajs, timestamps)
# sorted_trajectories is a DataFrame containing all trajectory samples
# sorted first by `object_id` and then by `timestamp`.
print(sorted_trajectories.head())
# trajectory_offsets is a Series containing the start position of each
# trajectory in sorted_trajectories.
print(trajectory_offsets)
object_id x y timestamp
0 1 0.680146 0.874341 1970-01-01 00:00:00.125
1 1 0.843522 0.044402 1970-01-01 00:00:00.834
2 1 0.837039 0.351025 1970-01-01 00:00:01.335
3 1 0.946184 0.479038 1970-01-01 00:00:01.791
4 1 0.117322 0.182117 1970-01-01 00:00:02.474
0 0
1 2455
2 4899
3 7422
4 9924
...
394 987408
395 989891
396 992428
397 994975
398 997448
Length: 399, dtype: int32
derive_trajectories sorts the trajectories by object_id, then timestamp, and returns acuspatial.trajectory_distances_and_speeds#
trajectory_distance_and_speed to calculate the overall distance travelled in meters andderive_trajectories.[8]:
trajs = cuspatial.GeoSeries.from_points_xy(
sorted_trajectories[["x", "y"]].interleave_columns()
)
d_and_s = cuspatial.core.trajectory.trajectory_distances_and_speeds(
len(cudf.Series(ids).unique()),
sorted_trajectories['object_id'],
trajs,
sorted_trajectories['timestamp']
)
print(d_and_s.head())
distance speed
trajectory_id
0 1.278996e+06 1280.320089
1 1.267179e+06 1268.370390
2 1.294437e+06 1295.905261
3 1.323413e+06 1323.956714
4 1.309590e+06 1311.561012
Bounding#
Compute the bounding boxes of n polygons or linestrings:

cuspatial.trajectory_bounding_boxes#
trajectory_bounding_boxes works out of the box with the values returned by derive_trajectories.[9]:
bounding_boxes = cuspatial.core.trajectory.trajectory_bounding_boxes(
len(cudf.Series(ids, dtype="int32").unique()),
sorted_trajectories['object_id'],
trajs
)
print(bounding_boxes.head())
x_min y_min x_max y_max
0 0.000098 0.000243 0.999422 0.999068
1 0.000663 0.000414 0.999813 0.998456
2 0.000049 0.000220 0.999748 0.999220
3 0.000006 0.000303 0.999729 0.999762
4 0.001190 0.000074 0.999299 0.999858
cuspatial.polygon_bounding_boxes#
polygon_bounding_boxes supports more complex geometry objects such as Polygons with multiplepart_offset and ring_offset allows the function to use only the[10]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
single_polygons = cuspatial.from_geopandas(
host_dataframe['geometry'][host_dataframe['geometry'].type == "Polygon"]
)
bounding_box_polygons = cuspatial.core.spatial.bounding.polygon_bounding_boxes(
single_polygons
)
print(bounding_box_polygons.head())
minx miny maxx maxy
0 29.339998 -11.720938 40.316590 -0.950000
1 -17.063423 20.999752 -8.665124 27.656426
2 46.466446 40.662325 87.359970 55.385250
3 55.928917 37.144994 73.055417 45.586804
4 12.182337 -13.257227 31.174149 5.256088
/tmp/ipykernel_5364/1016569337.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
cuspatial.linestring_bounding_boxes#
[11]:
lines = cuspatial.GeoSeries.from_linestrings_xy(
trajs.points.xy, trajectory_offsets, cupy.arange(len(trajectory_offsets))
)
trajectory_bounding_boxes = cuspatial.core.spatial.bounding.linestring_bounding_boxes(
lines, 0.0001
)
print(trajectory_bounding_boxes.head())
minx miny maxx maxy
0 -0.000002 0.000143 0.999522 0.999168
1 0.000563 0.000314 0.999913 0.998556
2 -0.000051 0.000120 0.999848 0.999320
3 -0.000094 0.000203 0.999829 0.999862
4 0.001090 -0.000026 0.999399 0.999958
Projection#
cuspatial.sinusoidal_projection#
[12]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
afghanistan = gpu_dataframe['geometry'][gpu_dataframe['name'] == 'Afghanistan']
points = cuspatial.GeoSeries.from_points_xy(afghanistan.polygons.xy)
projected = cuspatial.sinusoidal_projection(
afghanistan.polygons.x.mean(),
afghanistan.polygons.y.mean(),
points
)
print(projected.head())
0 POINT (112.174 -281.590)
1 POINT (62.152 -280.852)
2 POINT (-5.573 -257.391)
3 POINT (-33.071 -243.849)
4 POINT (-98.002 -279.540)
dtype: geometry
/tmp/ipykernel_5364/2658722012.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
Distance#
haversine and pairwise_linestring.hausdorff clustering distances algorithm is also available, computing the hausdorffcuspatial.directed_hausdorff_distance#
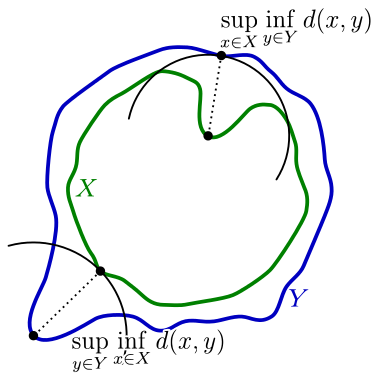
[13]:
coordinates = sorted_trajectories[['x', 'y']].interleave_columns()
spaces = cuspatial.GeoSeries.from_multipoints_xy(
coordinates, trajectory_offsets
)
hausdorff_distances = cuspatial.core.spatial.distance.directed_hausdorff_distance(
spaces
)
print(hausdorff_distances.head())
0 1 2 3 4 5 6 \
0 0.000000 0.034755 0.031989 0.031959 0.031873 0.038674 0.029961
1 0.030328 0.000000 0.038672 0.032086 0.031049 0.032170 0.032275
2 0.027640 0.030539 0.000000 0.036737 0.033055 0.043447 0.028812
3 0.031497 0.033380 0.035224 0.000000 0.032581 0.035484 0.030339
4 0.031079 0.032256 0.035731 0.039084 0.000000 0.036416 0.031369
7 8 9 ... 388 389 390 391 \
0 0.029117 0.040962 0.033259 ... 0.031614 0.036447 0.035548 0.028233
1 0.030215 0.034443 0.032998 ... 0.030594 0.035665 0.031473 0.031916
2 0.031807 0.039269 0.033250 ... 0.031998 0.033636 0.034646 0.032615
3 0.034792 0.045755 0.031810 ... 0.033623 0.031359 0.034923 0.032287
4 0.030388 0.033751 0.034029 ... 0.030705 0.040339 0.034328 0.029027
392 393 394 395 396 397
0 0.034176 0.030057 0.033863 0.031111 0.034590 0.033850
1 0.037483 0.033489 0.041403 0.029784 0.035374 0.038179
2 0.036681 0.030642 0.038432 0.032481 0.034810 0.036695
3 0.032808 0.029771 0.040891 0.030802 0.032279 0.038443
4 0.035645 0.027703 0.037529 0.029356 0.031260 0.035501
[5 rows x 398 columns]
cuspatial.haversine_distance#
lon/lat ordering to better reflect the cartesian coordinates of great circlex/y.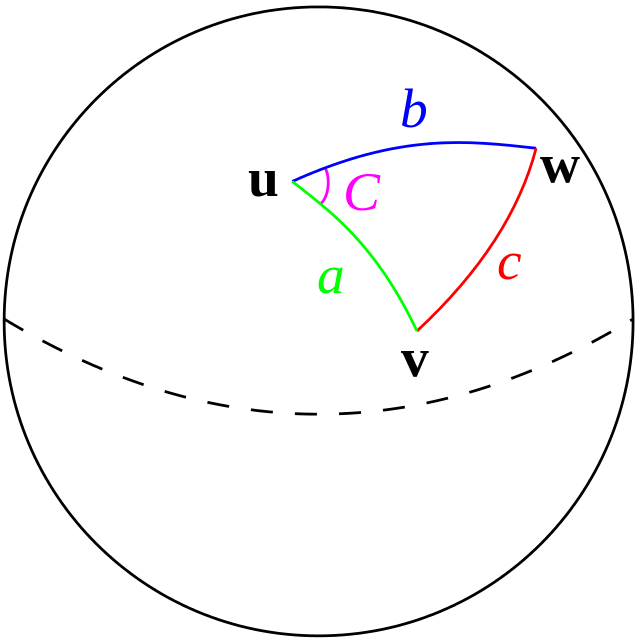
[14]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
polygons_first = gpu_dataframe['geometry'][0:10]
polygons_second = gpu_dataframe['geometry'][10:20]
points_first = polygons_first.polygons.xy[0:1000]
points_second = polygons_second.polygons.xy[0:1000]
first = cuspatial.GeoSeries.from_points_xy(points_first)
second = cuspatial.GeoSeries.from_points_xy(points_second)
# The number of coordinates in two sets of polygons vary, so
# we'll just compare the first set of 1000 values here.
distances_in_meters = cuspatial.haversine_distance(
first, second
)
cudf.Series(distances_in_meters).head()
/tmp/ipykernel_5364/491857862.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
[14]:
0 9959.695143
1 9803.166859
2 9876.857085
3 9925.097106
4 9927.268486
Name: None, dtype: float64
This above method reads the GeoPandas data from CPU memory into GPU memory and then cuSpatial processes it. If the data is already in a cuDF GPU dataframe, you can quickly calculate Haversine distances using the method below. This maximizes speed by keeping all the processing on the GPU and is very useful when working on large datasets.
[15]:
# Generate data to be used to create a cuDF dataframe.
# The data to be processed by Haversine MUST be a Float.
a = {"latitude":[17.1167, 17.1333, 25.333, 25.255, 24.433, 24.262, 35.317, 34.21, 34.566, 31.5, 36.7167, 30.5667, 28.05, 22.8, 35.7297, 36.97, 36.78, 36.8, 36.8, 36.72],
"longitude": [-61.7833, -61.7833, 55.517, 55.364, 54.651, 55.609, 69.017, 62.228, 69.212, 65.85, 3.25, 2.8667, 9.6331, 5.4331, 0.65, 7.79, 3.07, 3.03, 3.04, 4.05]}
df = cudf.DataFrame(data=a)
# Create cuSpatial GeoSeries from cuDF Dataframe
cuGeoSeries = cuspatial.GeoSeries.from_points_xy(df[['longitude', 'latitude']].interleave_columns())
# Create Comparator cuSpatial GeoSeries from a comparator point
df['atlanta_lat'] = 33.7490
df['atlanta_lng'] = -84.3880
atlGeoSeries = cuspatial.GeoSeries.from_points_xy(df[['atlanta_lat', 'atlanta_lng']].interleave_columns())
# Calculate Haversine Distance of cuDF dataframe to comparator point
df['atlanta_dist'] = cuspatial.haversine_distance(cuGeoSeries, atlGeoSeries)
print(df.head())
latitude longitude atlanta_lat atlanta_lng atlanta_dist
0 17.1167 -61.7833 33.749 -84.388 11961.556540
1 17.1333 -61.7833 33.749 -84.388 11963.392729
2 25.3330 55.5170 33.749 -84.388 12243.126130
3 25.2550 55.3640 33.749 -84.388 12233.867463
4 24.4330 54.6510 33.749 -84.388 12139.822218
5 24.2620 55.6090 33.749 -84.388 12124.483127
6 35.3170 69.0170 33.749 -84.388 13418.538383
7 34.2100 62.2280 33.749 -84.388 13258.725239
8 34.5660 69.2120 33.749 -84.388 13336.375942
9 31.5000 65.8500 33.749 -84.388 12976.749248
10 36.7167 3.2500 33.749 -84.388 13547.245294
11 30.5667 2.8667 33.749 -84.388 12866.528267
12 28.0500 9.6331 33.749 -84.388 12554.544289
13 22.8000 5.4331 33.749 -84.388 11990.825098
14 35.7297 0.6500 33.749 -84.388 13451.775999
15 36.9700 7.7900 33.749 -84.388 13553.372737
16 36.7800 3.0700 33.749 -84.388 13555.211584
17 36.8000 3.0300 33.749 -84.388 13557.641136
18 36.8000 3.0400 33.749 -84.388 13557.588738
19 36.7200 4.0500 33.749 -84.388 13543.496327
Pairwise distance#
pairwise_linestring_distance computes the distance between a GeoSeries of Linestrings ofn and a corresponding GeoSeries of Linestrings of n length. It returns theThe input accepts a pair of geoseries as input sequences of linestring arrays.
naturalearth_lowres and treats them as linestrings.cuspatial.pairwise_linestring_distance#
[16]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_boundaries = cuspatial.from_geopandas(host_dataframe.geometry.boundary)
zeros = cuspatial.pairwise_linestring_distance(
gpu_boundaries[0:50],
gpu_boundaries[0:50]
)
print(zeros.head())
lines1 = gpu_boundaries[0:50]
lines2 = gpu_boundaries[50:100]
distances = cuspatial.pairwise_linestring_distance(
lines1, lines2
)
print(distances.head())
/tmp/ipykernel_5364/1097934054.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
0 0.0
1 0.0
2 0.0
3 0.0
4 0.0
dtype: float64
0 152.200610
1 44.076445
2 2.417269
3 44.197151
4 75.821029
dtype: float64
pairwise_point_linestring_distance computes the distance between pairs of points andcuspatial.pairwise_point_linestring_distance#
Using WGS 84 Pseudo-Mercator, distances are in meters.
[17]:
# Convert input dataframe to Pseudo-Mercator projection.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
polygons = host_dataframe[host_dataframe['geometry'].type == "Polygon"]
gpu_polygons = cuspatial.from_geopandas(polygons)
# Extract mean_x and mean_y from each country
mean_x = [gpu_polygons['geometry'].iloc[[ix]].polygons.x.mean() for ix in range(len(gpu_polygons))]
mean_y = [gpu_polygons['geometry'].iloc[[ix]].polygons.y.mean() for ix in range(len(gpu_polygons))]
# Convert mean_x/mean_y values into Points for use in API.
points = cuspatial.GeoSeries([Point(point) for point in zip(mean_x, mean_y)])
# Convert Polygons into Linestrings for use in API.
linestring_df = cuspatial.from_geopandas(geopandas.geoseries.GeoSeries(
[MultiLineString(mapping(polygons['geometry'].iloc[ix])["coordinates"]) for ix in range(len(polygons))]
))
gpu_polygons['border_distance'] = cuspatial.pairwise_point_linestring_distance(
points, linestring_df
)
print(gpu_polygons.head())
/tmp/ipykernel_5364/2846028812.py:2: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
pop_est continent name iso_a3 gdp_md_est \
1 58005463.0 Africa Tanzania TZA 63177
2 603253.0 Africa W. Sahara ESH 907
5 18513930.0 Asia Kazakhstan KAZ 181665
6 33580650.0 Asia Uzbekistan UZB 57921
11 86790567.0 Africa Dem. Rep. Congo COD 50400
geometry border_distance
1 POLYGON ((3774143.866 -105758.362, 3792946.708... 8047.288391
2 POLYGON ((-964649.018 3205725.605, -964597.245... 593137.492497
5 POLYGON ((9724867.413 6311418.173, 9640131.701... 37091.213890
6 POLYGON ((6230350.563 5057973.384, 6225978.591... 278633.467299
11 POLYGON ((3266113.592 -501451.658, 3286149.877... 35812.988244
(GPU)
cuspatial.pairwise_point_polygon_distance#
Using WGS 84 Pseudo-Mercator, distances are in meters.
[18]:
cities = geopandas.read_file(geopandas.datasets.get_path("naturalearth_cities")).to_crs(3857)
countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
gpu_cities = cuspatial.from_geopandas(cities)
gpu_countries = cuspatial.from_geopandas(countries)
dist = cuspatial.pairwise_point_polygon_distance(
gpu_cities.geometry[:len(gpu_countries)], gpu_countries.geometry
)
gpu_countries["distance_from"] = cities.name
gpu_countries["distance"] = dist
gpu_countries.head()
/tmp/ipykernel_5364/3261459244.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_cities' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
cities = geopandas.read_file(geopandas.datasets.get_path("naturalearth_cities")).to_crs(3857)
/tmp/ipykernel_5364/3261459244.py:2: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
[18]:
| pop_est | continent | name | iso_a3 | gdp_md_est | geometry | distance_from | distance | |
|---|---|---|---|---|---|---|---|---|
| 0 | 889953.0 | Oceania | Fiji | FJI | 5496 | MULTIPOLYGON (((20037508.343 -1812498.413, 200... | Vatican City | 1.969350e+07 |
| 1 | 58005463.0 | Africa | Tanzania | TZA | 63177 | POLYGON ((3774143.866 -105758.362, 3792946.708... | San Marino | 5.929777e+06 |
| 2 | 603253.0 | Africa | W. Sahara | ESH | 907 | POLYGON ((-964649.018 3205725.605, -964597.245... | Vaduz | 3.421172e+06 |
| 3 | 37589262.0 | North America | Canada | CAN | 1736425 | MULTIPOLYGON (((-13674486.249 6274861.394, -13... | Lobamba | 1.296059e+07 |
| 4 | 328239523.0 | North America | United States of America | USA | 21433226 | MULTIPOLYGON (((-13674486.249 6274861.394, -13... | Luxembourg | 8.174897e+06 |
cuspatial.pairwise_linestring_polygon_distance#
Using WGS 84 Pseudo-Mercator, distances are in meters.
[19]:
# all driveways within 2km range of central park, nyc
# The dataset is downloaded and processed as follows:
# import osmnx as ox
# graph = ox.graph_from_point((40.769361, -73.977655), dist=2000, network_type="drive")
# nodes, streets = ox.graph_to_gdfs(graph)
# streets = streets.to_crs(3857)
# streets = streets.reset_index(drop=True)
# streets.index.name = "index"
# streets[["name", "geometry"]].to_csv("streets_3857.csv")
# The data is under notebooks/streets_3857.csv
streets = pd.read_csv("./streets_3857.csv", index_col="index")
streets.geometry = streets.geometry.apply(wkt.loads)
streets = geopandas.GeoDataFrame(streets)
streets.head()
[19]:
| name | geometry | |
|---|---|---|
| index | ||
| 0 | Columbus Avenue | LINESTRING (-8234860.077 4980333.535, -8234863... |
| 1 | West 80th Street | LINESTRING (-8235173.854 4980508.442, -8235160... |
| 2 | Amsterdam Avenue | LINESTRING (-8235173.854 4980508.442, -8235168... |
| 3 | West 80th Street | LINESTRING (-8235369.475 4980617.398, -8235349... |
| 4 | Broadway | LINESTRING (-8235369.475 4980617.398, -8235373... |
[20]:
# The polygon of the Empire State Building
# The dataset is downloaded and processed as follows:
# esb = ox.geometries.geometries_from_place('Empire State Building, New York', tags={"building": True})
# esb = esb.to_crs(3857)
# esb = esb.geometry.reset_index(drop=True)
# esb.index.name = "index"
# esb.to_csv("esb_3857.csv")
# The data is under notebooks/esb_3857.csv
esb = pd.read_csv("./esb_3857.csv", index_col="index")
esb.geometry = esb.geometry.apply(wkt.loads)
esb = geopandas.GeoDataFrame(esb)
esb = pd.concat([esb.iloc[0:1]] * len(streets))
esb.head()
[20]:
| geometry | |
|---|---|
| index | |
| 0 | POLYGON ((-8236139.639 4975314.625, -8235990.3... |
| 0 | POLYGON ((-8236139.639 4975314.625, -8235990.3... |
| 0 | POLYGON ((-8236139.639 4975314.625, -8235990.3... |
| 0 | POLYGON ((-8236139.639 4975314.625, -8235990.3... |
| 0 | POLYGON ((-8236139.639 4975314.625, -8235990.3... |
[21]:
# Straight line distance between the driveways to the Empire State Building
gpu_streets = cuspatial.from_geopandas(streets.geometry)
gpu_esb = cuspatial.from_geopandas(esb.geometry)
dist = cuspatial.pairwise_linestring_polygon_distance(gpu_streets, gpu_esb).rename("dist")
pd.concat([streets["name"].reset_index(drop=True), dist.to_pandas()], axis=1)
[21]:
| name | dist | |
|---|---|---|
| 0 | Columbus Avenue | 4993.583717 |
| 1 | West 80th Street | 5103.472213 |
| 2 | Amsterdam Avenue | 5208.373183 |
| 3 | West 80th Street | 5276.886560 |
| 4 | Broadway | 5178.999774 |
| ... | ... | ... |
| 1859 | East 70th Street | 4193.471831 |
| 1860 | West 65th Street | 3999.118604 |
| 1861 | Dyer Avenue | 1470.617115 |
| 1862 | Dyer Avenue | 1468.714127 |
| 1863 | Dyer Avenue | 1548.205363 |
1864 rows × 2 columns
cuspatial.pairwise_polygon_distance#
Using WGS 84 Pseudo-Mercator, distances are in meters.
[22]:
countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
gpu_countries = cuspatial.from_geopandas(countries)
african_countries = gpu_countries[gpu_countries.continent == "Africa"].sort_values("pop_est", ascending=False)
asian_countries = gpu_countries[gpu_countries.continent == "Asia"].sort_values("pop_est", ascending=False)
/tmp/ipykernel_5364/3213563529.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres")).to_crs(3857)
[23]:
# Straight line distance between the top 10 most populated countries in Asia and Africa
population_top10_africa = african_countries[:10].reset_index(drop=True)
population_top10_asia = asian_countries[:10].reset_index(drop=True)
dist = cuspatial.pairwise_polygon_distance(
population_top10_africa.geometry, population_top10_asia.geometry)
cudf.concat([
population_top10_africa["name"].rename("Africa"),
population_top10_asia["name"].rename("Asia"),
dist.rename("dist")], axis=1
)
[23]:
| Africa | Asia | dist | |
|---|---|---|---|
| 0 | Nigeria | China | 7.383366e+06 |
| 1 | Ethiopia | India | 2.883313e+06 |
| 2 | Egypt | Indonesia | 6.776043e+06 |
| 3 | Dem. Rep. Congo | Pakistan | 4.227767e+06 |
| 4 | South Africa | Bangladesh | 8.189086e+06 |
| 5 | Tanzania | Japan | 1.096947e+07 |
| 6 | Kenya | Philippines | 8.399282e+06 |
| 7 | Uganda | Vietnam | 7.773975e+06 |
| 8 | Algeria | Turkey | 2.000180e+06 |
| 9 | Sudan | Iran | 1.625828e+06 |
Filtering#
The filtering module contains points_in_spatial_window, which returns from a set of points only those points that fall within a spatial window defined by four bounding coordinates: min_x, max_x, min_y, and max_y. The following example finds only the points of polygons that fall within 1 standard deviation of the mean of all of the polygons.
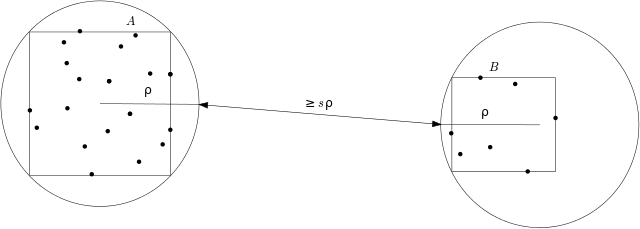
cuspatial.points_in_spatial_window#
[24]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
gpu_dataframe = cuspatial.from_geopandas(host_dataframe)
geometry = gpu_dataframe['geometry']
points = cuspatial.GeoSeries.from_points_xy(geometry.polygons.xy)
mean_x, std_x = (geometry.polygons.x.mean(), geometry.polygons.x.std())
mean_y, std_y = (geometry.polygons.y.mean(), geometry.polygons.y.std())
avg_points = cuspatial.points_in_spatial_window(
points,
mean_x - std_x,
mean_x + std_x,
mean_y - std_y,
mean_y + std_y
)
print(avg_points.head())
/tmp/ipykernel_5364/3414785716.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
0 POINT (33.90371 -0.95000)
1 POINT (34.07262 -1.05982)
2 POINT (37.69869 -3.09699)
3 POINT (37.76690 -3.67712)
4 POINT (39.20222 -4.67677)
dtype: geometry
With some careful grouping, one can reconstruct the original complete polygons that fall within the range.
Set Operations#
Linestring Intersections#
cuSpatial provides a linestring-linestring intersection algorithm to compute the overlapping geometries between two linestrings. The API also returns the ids for each returned geometry to help user to trace back the source geometry.
[25]:
from cuspatial.core.binops.intersection import pairwise_linestring_intersection
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
usa_boundary = cuspatial.from_geopandas(host_dataframe[host_dataframe.name == "United States of America"].geometry.boundary)
canada_boundary = cuspatial.from_geopandas(host_dataframe[host_dataframe.name == "Canada"].geometry.boundary)
list_offsets, geometries, look_back_ids = pairwise_linestring_intersection(usa_boundary, canada_boundary)
/tmp/ipykernel_5364/199363072.py:3: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
[26]:
# The first integer series shows that the result contains 1 row (since we only have 1 pair of linestrings as input).
# This row contains 144 geometires.
list_offsets
[26]:
<cudf.core.column.numerical.NumericalColumn object at 0x7f2c5a872d40>
[
0,
142
]
dtype: int32
[27]:
# The second element is a geoseries that contains the intersecting geometries, with 144 rows, including points and linestrings.
geometries
[27]:
0 POINT (-130.53611 54.80275)
1 POINT (-130.53611 54.80278)
2 POINT (-130.53611 54.80275)
3 POINT (-129.98000 55.28500)
4 POINT (-130.53611 54.80278)
...
137 LINESTRING (-120.00000 49.00000, -117.03121 49...
138 LINESTRING (-122.84000 49.00000, -120.00000 49...
139 LINESTRING (-117.03121 49.00000, -107.05000 49...
140 LINESTRING (-83.89077 46.11693, -83.61613 46.1...
141 LINESTRING (-82.69009 41.67511, -82.43928 41.6...
Length: 142, dtype: geometry
[28]:
# The third element is a dataframe that contains IDs to the input segments and linestrings, 4 for each result row.
# Each represents ids to lhs, rhs linestring and segment ids.
look_back_ids
[28]:
| lhs_linestring_id | lhs_segment_id | rhs_linestring_id | rhs_segment_id | |
|---|---|---|---|---|
| 0 | [8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, ... | [18, 16, 18, 15, 17, 14, 16, 13, 15, 14, 11, 1... | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... | [9, 10, 10, 11, 11, 12, 12, 13, 13, 14, 15, 15... |
Spatial Joins#
cuSpatial provides a number of functions to facilitate high-performance spatial joins, including unindexed and quadtree-indexed point-in-polygon and quadtree-indexed point to nearest linestring.
The API for spatial joins does not yet match GeoPandas, but with knowledge of cuSpatial data formats you can call cuspatial.point_in_polygon for large numbers of points on 32 polygons or less, or call cuspatial.quadtree_point_in_polygon for large numbers of points and polygons.
Unindexed Point-in-polygon Join#
cuspatial.point_in_polygon#
[29]:
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
single_polygons = host_dataframe[host_dataframe['geometry'].type == "Polygon"]
gpu_dataframe = cuspatial.from_geopandas(single_polygons)
x_points = (cupy.random.random(10000000) - 0.5) * 360
y_points = (cupy.random.random(10000000) - 0.5) * 180
xy = cudf.DataFrame({"x": x_points, "y": y_points}).interleave_columns()
points = cuspatial.GeoSeries.from_points_xy(xy)
short_dataframe = gpu_dataframe.iloc[0:31]
geometry = short_dataframe['geometry']
points_in_polygon = cuspatial.point_in_polygon(
points, geometry
)
sum_of_points_in_polygons_0_to_31 = points_in_polygon.sum()
sum_of_points_in_polygons_0_to_31.head()
/tmp/ipykernel_5364/1271339229.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_dataframe = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
[29]:
1 11896
2 1268
5 50835
6 7792
11 29318
dtype: int64
quadtree_point_in_polygon that uses an indexingquadtree_point_in_polygon also supports a number ofQuadtree Indexing#
The indexing module is used to create a spatial quadtree. Use
cuspatial.quadtree_on_points(
points,
x_min,
x_max,
y_min,
y_max,
scale,
max_depth,
max_size
)
quadtree_point_in_polygonjoin module.scale: A scaling function that increases the size of the point space from an{x_min, y_min}. This can increase the likelihood of generatingmax_depth: In order for a quadtree to index points effectively, it must have a depth that is log-scaled with the size of the number of points. Each level of themax_depth parameter. With an input size10m points and max_depth = 7, \(\frac{10^6}{4^7}\) points will be mostmax_size: The maximum number of points allowed in an internal node before it is split into four leaf notes. As the quadtree is generated, a leaf node containing usable index points will be created as points are added. If the number of points in this leaf exceeds max_size, the leaf will be subdivided, with four new leaves added and the original node removed from the set of leaves. This number is probably optimized in most datasets by making it a significant fraction of the optimal leaf
size computation from above. Consider \(10,000,000 / 4^7 / 4 = 153\).
cuspatial.quadtree_on_points#
[30]:
x_points = (cupy.random.random(10000000) - 0.5) * 360
y_points = (cupy.random.random(10000000) - 0.5) * 180
xy = cudf.DataFrame({"x": x_points, "y": y_points}).interleave_columns()
points = cuspatial.GeoSeries.from_points_xy(xy)
scale = 5
max_depth = 7
max_size = 125
point_indices, quadtree = cuspatial.quadtree_on_points(points,
x_points.min(),
x_points.max(),
y_points.min(),
y_points.max(),
scale,
max_depth,
max_size)
print(point_indices.head())
print(quadtree.head())
0 1507
1 1726
2 4242
3 7371
4 11341
dtype: uint32
key level is_internal_node length offset
0 0 0 True 4 2
1 1 0 True 2 6
2 0 1 True 4 8
3 1 1 True 4 12
4 2 1 True 2 16
Indexed Spatial Joins#
The quadtree spatial index (point_indices and quadtree) is used by quadtree_point_in_polygon and quadtree_point_to_nearest_linestring to accelerate larger spatial joins. quadtree_point_in_polygon depends on a number of intermediate products calculated here using the following functions.
cuspatial.join_quadtree_and_bounding_boxes#
cuspatial.quadtree_point_in_polygon#
[31]:
polygons = gpu_dataframe['geometry']
poly_bboxes = cuspatial.polygon_bounding_boxes(
polygons
)
intersections = cuspatial.join_quadtree_and_bounding_boxes(
quadtree,
poly_bboxes,
polygons.polygons.x.min(),
polygons.polygons.x.max(),
polygons.polygons.y.min(),
polygons.polygons.y.max(),
scale,
max_depth
)
polygons_and_points = cuspatial.quadtree_point_in_polygon(
intersections,
quadtree,
point_indices,
points,
polygons
)
print(polygons_and_points.head())
Empty DataFrame
Columns: [polygon_index, point_index]
Index: []
cuspatial.quadtree_point_to_nearest_linestring#
cuspatial.quadtree_point_to_nearest_linestring can be used to find the Polygon or Linestring[32]:
host_countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
host_cities = geopandas.read_file(geopandas.datasets.get_path("naturalearth_cities"))
gpu_countries = cuspatial.from_geopandas(host_countries[host_countries['geometry'].type == "Polygon"])
gpu_cities = cuspatial.from_geopandas(host_cities[host_cities['geometry'].type == 'Point'])
/tmp/ipykernel_5364/2951982051.py:1: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_lowres' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_countries = geopandas.read_file(geopandas.datasets.get_path("naturalearth_lowres"))
/tmp/ipykernel_5364/2951982051.py:2: FutureWarning: The geopandas.dataset module is deprecated and will be removed in GeoPandas 1.0. You can get the original 'naturalearth_cities' data from https://www.naturalearthdata.com/downloads/110m-cultural-vectors/.
host_cities = geopandas.read_file(geopandas.datasets.get_path("naturalearth_cities"))
[33]:
polygons = gpu_countries['geometry'].polygons
boundaries = cuspatial.GeoSeries.from_linestrings_xy(
cudf.DataFrame({"x": polygons.x, "y": polygons.y}).interleave_columns(),
polygons.ring_offset,
cupy.arange(len(polygons.ring_offset))
)
point_indices, quadtree = cuspatial.quadtree_on_points(gpu_cities['geometry'],
polygons.x.min(),
polygons.x.max(),
polygons.y.min(),
polygons.y.max(),
scale,
max_depth,
max_size)
poly_bboxes = cuspatial.linestring_bounding_boxes(
boundaries,
2.0
)
intersections = cuspatial.join_quadtree_and_bounding_boxes(
quadtree,
poly_bboxes,
polygons.x.min(),
polygons.x.max(),
polygons.y.min(),
polygons.y.max(),
scale,
max_depth
)
result = cuspatial.quadtree_point_to_nearest_linestring(
intersections,
quadtree,
point_indices,
gpu_cities['geometry'],
boundaries
)
print(result.head())
point_index linestring_index distance
0 0 21 10.857363
1 1 21 10.937690
2 2 19 0.522859
3 3 19 0.050204
4 4 129 0.104261
Images used with permission from Wikipedia Creative Commons